理论介绍:
矩阵的迹运算自然来源于（几何或代数的）不变量理论 (invariant theory)。 对于一般的张量空间，迹运算可以构造出所有的不变量。
迹运算返回的矩阵对角元素的和：
迹运算因为很多原因而受到关注。若不使用求和符号，有些矩阵运算很难描述，而通过矩阵乘法和迹运算符号，可以清楚地表示。例如，迹运算提供了另一种描述矩阵robeniusFrobenius 范数的方式：
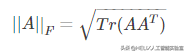
Frobenius 范数，即矩阵元素绝对值的平方和再开平方。
用迹运算表示表达式，我们可以使用很多有用的等式来操纵表达式。例如，迹运算在转置运算下是不变的：
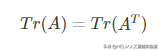
多个矩阵乘积的迹，和将这些矩阵中最后一个挪到最前面之后乘积的迹是相同的。当然，我们需要考虑挪动之后矩阵乘积依然定义良好：
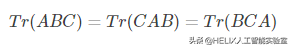
即使循环置换后矩阵乘积得到的矩阵形状变了，迹运算的结果依然不变。例如，假设矩阵A∈Rm×nA∈Rm×n，矩阵B∈Rn×mB∈Rn×m，我们可以得到:
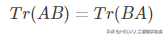
即使AB∈Rm×mAB∈Rm×m和BA∈Rn×nBA∈Rn×n。
另一个有用的事实是标量在迹运算后仍然是它自己：a=Tr(a)a=Tr(a)。
应用意义：
在线性代数中，一个n×n的对角矩阵A的主对角线（从左上方至右下方的对角线）上各个元素的总和被称为矩阵A的迹（或迹数），一般记作tr(A)。
例子如下：
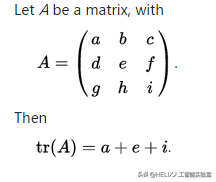
对角元素是a,e,i，这三者之和就叫矩阵的迹。
我一直在想，为什么非要抓住这个矩阵的对角线不放呢？难道有什么高深的学问吗？
后来仔细一想，矩阵的对角线可以表示一个物体的相似性，比如在图形学的缩放变换里使用的矩阵是这样的：
在这里可以看到就是对角的元素表示缩放，那么表示物体具有相似性。
在机器学习里，主要为了获取数据的特征值，那么就是说，在任何一个矩阵计算出来之后，都可以简单化，只要获取矩阵的迹，就可以表示这一块数据的最重要的特征了，这样就可以把很多无关紧要的数据删除掉，达到简化数据，提高处理速度。
--------------------
相关文章：
夏普中央空调售后维修热线|网点查询（夏普中央空调空调多少瓦 ）07-12
广优中央空调售后维修号码-人工售后号码实时反馈-今-日-资-讯（广优中央空调空调控制器 ）07-12
月兔空调售后号码多少实时反馈全+境+到+达（月兔空调空调怎么制冷 ）07-12
本科空调客服人工号码(全国统一)400客服热线实时反馈-今-日-汇-总（本科空调灰尘传感器故障 ）07-12
长虹风管机售后号码多少实时反馈-今-日-更-新（长虹风管机空调外机滴水 ）07-12
艾尔韦尔中央空调服务号码24小时(今日更新)实时反馈-今-日-汇-总（艾尔韦尔中央空调空调e4 ）07-12